ですが、次の方法で簡単に計算することができます。 円すいの側面積 = 母線 × 半径 × π 5 × 3 × π = 15 π c m 2 問題表面積を求めなさい。 表面積 = 側面積 底面積 底面積は 9 π c m 2 、側面積は 15 π c m 2 よって、表面積は 15 π 9 π = 24 π c m 2相似比を3乗することで求めてやることができます。 つまり 相似比がわかれば 体積比はすーぐに求めることができるということですね！ それでは、さっきの円錐の問題を考えてみましょう。 円錐問題の考え方 円錐を2つに分けた図形の体積比を考えるの · 円錐の体積比の計算問題を解いてみよう それでは、塩水の相似比、面積比、体積比の算出に慣れるためにも、練習問題を解いていきましょう。 例題 辺の長さの比（相似比）が3：2である円錐の体積比はいくつになるでしょうか。 解答
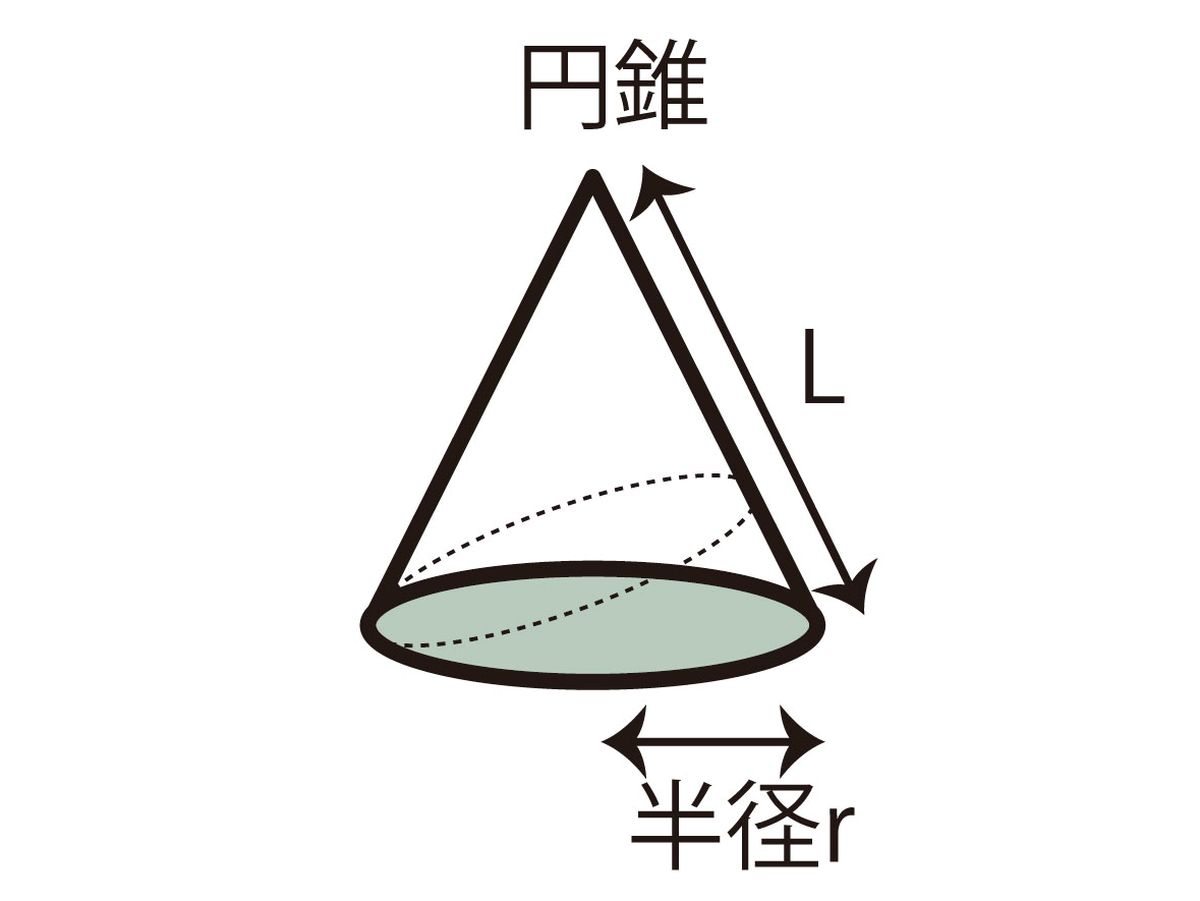
円錐の側面積の公式を理解させる方法 オンライン授業専門塾ファイ
扇形の弧の長さの求め方 公式と計算例 扇形の弧の長さを求める公式は、次の通りです。 l = 2πr× x 360 l = 2 π r × x 360 中心角 x 扇形の中心角を求める公式は、 x = 180 × 弧の長さ π × 半径 x = 180 × 弧 の 長 さ π × 半 径 弧の長さ= L、半径= r とすると、 x = 180L πr x = 180 L π r だよ 公式は忘れちゃったら解けないし、これを覚えるのは大変だよ だから、きっちり 本質 を理解しようね扇形 の 中心 角 の 求め 方 公式。 高校数学"扇形の弧の長さと面積"の公式とその証明 」） ほか、道路、警察、消防署、公園など身近な施設を想像してください。 be動詞＋過去分詞で使います。 11 important;webkitboxsizingborderbox!
扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
長方形の面積 長方形の面積の求め方はよく知っていると思います。 一番簡単な公式ですね。 長方形の面積＝たて×よこ 特に問題はないですね？ このあとにでてくる 平行四辺形 三 » この記事の続き
円柱の表面積の求め方
基本：表面積の求め方 立体の表面積とは、表側にある面の面積をすべて足したものをいいます。 イメージとしては、空気にふれてる面ぜんぶってこと。 だから、基本となる求め方は 展開図をかいて求める というものです。 以下、例題とともに見ていきましょう。 角柱の表面積 19 神奈川132 次の図の三角柱の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 学基本学習の基本 32 角柱・円柱の体積と表面積 ① 立体のすべての面の面積の和を表面積という。また，側面全体の面積を側面積，1 つの底面の 面積を底面積という。
